Difference between revisions of "Servo tuning basics"
| [checked revision] | [checked revision] |
| (14 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Driving a servo motor is much like driving a car. Driving a car has many similarities including the key concepts of torque, velocity and position control. Most of this happens in the driver's head the same way than a servo drive does with a motor. | + | {{parent|Servo motor tuning guide}}Driving a servo motor is much like driving a car. Driving a car has many similarities including the key concepts of torque, velocity and position control. Most of this happens in the driver's head the same way than a servo drive does with a motor. |
| − | ==Driving (a.k.a servoing) a car== | + | |
| + | For those who are already familiar with the basics, see the principles of real world servo motor drive from article [[Signal path of motor drive]]. | ||
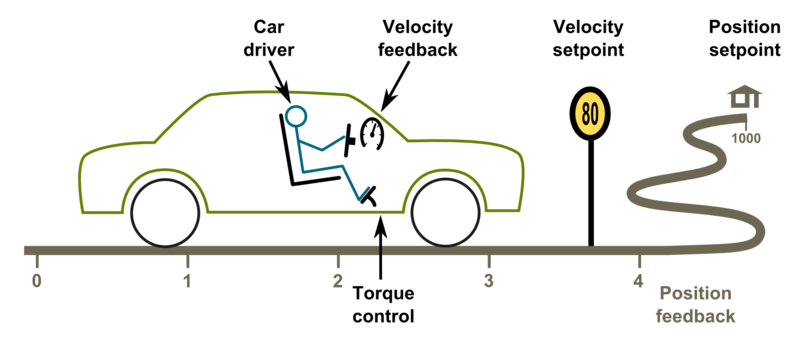
| + | ==Driving (a.k.a servoing) a car== | ||
| + | Driving a car to a destination is much like driving a servo motor to it's destination position. The analogies in between are: | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Car !! Servo axis | ||
| + | |- | ||
| + | | Pedal (motor gasoline feed) || Torque setpoint (motor current feed) | ||
| + | |- | ||
| + | | Speed limit || Velocity setpoint | ||
| + | |- | ||
| + | | Target location || Position setpoint | ||
| + | |- | ||
| + | | Speed meter || Velocity feedback | ||
| + | |- | ||
| + | | Trip meter|| Position feedback | ||
| + | |- | ||
| + | | Car driver || Servo drive | ||
| + | |} | ||
| + | |||
[[File:Carexample base.png|800px]] | [[File:Carexample base.png|800px]] | ||
| − | + | The ultimate goal of driver is to get to the target. To achieve this, he follows the road (trajectory) at certain velocity and decelerates once target is being reached. Without knowing, the driver acts as servo controller where he: | |
| − | + | *Controls car's velocity based on the speed meter value and speed limit | |
| − | + | *Controls car's position based on trip meter's reading or by observing location trough the windshield | |
| + | *All actions the driver makes, is based on comparing the setpoints and the actual state | ||
| − | + | ==Servo controller basics== | |
| + | ===Controller gains and a PI controller=== | ||
| + | Controller gain means '''sensitivity to change output''' due to ''tracking error'' (the difference between setpoint and feedback). | ||
| − | + | The simplest form of feedback based controller is a '''proportional''' gain controller (P controller) where output follows the formula ''output = Pgain*(setpoint-feedback)''. The problem of proportional gain controller is that it may never reach the setpoint because output starts approaching zero when the following error is reaching zero. | |
| − | The characteristics of gain variables: | + | Because of this, it's better to add in '''integrating''' component to the controller (forming PI controller). Integrator accumulates the tracking error to a integrator variable. Integrator variable is like a bucket of water, when you add water, the water level rises and when you take out water, the level lowers. In controller the equation becomes: ''output = Pgain*(setpoint-feedback) + Igain*IntegralOf(setpoint-feedback)''. |
| + | |||
| + | The characteristics of feedback gain variables: | ||
*P-gain - reacts instantly to the tracking error but can't eliminate tracking error completely | *P-gain - reacts instantly to the tracking error but can't eliminate tracking error completely | ||
| − | *I-gain - reacts slowly over time | + | *I-gain - reacts slowly over time, adjusts output until tracking error is zero |
| − | === | + | When driving a car, human brain closely resembles the operation of a PI controller. For in-depth info about PI controllers and its variants, see the Wikipedia article [http://en.wikipedia.org/wiki/PID_controller PID controller]. |
| + | |||
| + | ===Tuning the gains=== | ||
| + | Controller tuning means finding of the optimum gain values for the given system. | ||
| + | |||
| + | The proper gain values always depend on many aspects, especially the target system dynamic properties (such as motor properties, axis transmission ratios, inertias and masses). Change of properties introduces the requirement of tuning the gain values as gain values that work fine in one system may not behave satisfactory on a different system. | ||
| + | |||
| + | In servo drive case, this means that each motor type and mechanical axis need to be tuned separately. However, if axis and motors are identical, then the same gains should work equally. | ||
| + | |||
| + | ==Gain tuning (car) example== | ||
| + | The following series of images illustrate an imaginary car driving scenario where the driver acts as velocity controller of the car. The magnitude of PI gain values equal the driver's aggressivity of controlling the pedal to reach the desired speed. | ||
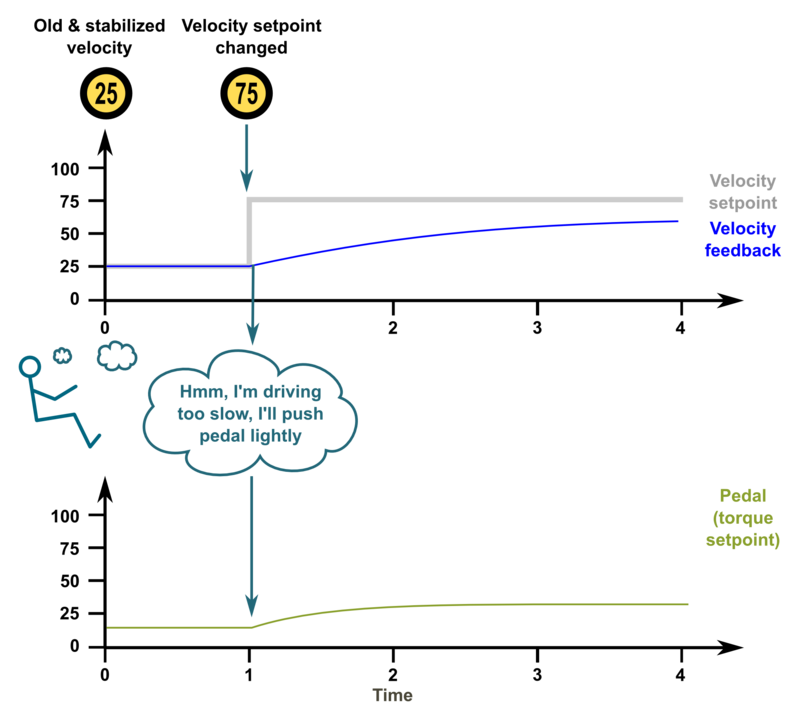
| + | ===Low gains - sluggish response=== | ||
[[File:Carexample sluggish.png|800px]] | [[File:Carexample sluggish.png|800px]] | ||
| − | ===Too high | + | |
| + | If the gains are set too low, the system response tends to be sluggish and sometimes leave a static tracking error (not reaching setpoint in any time). In this imaginary case we could think PI gains to be P=20 I=10. | ||
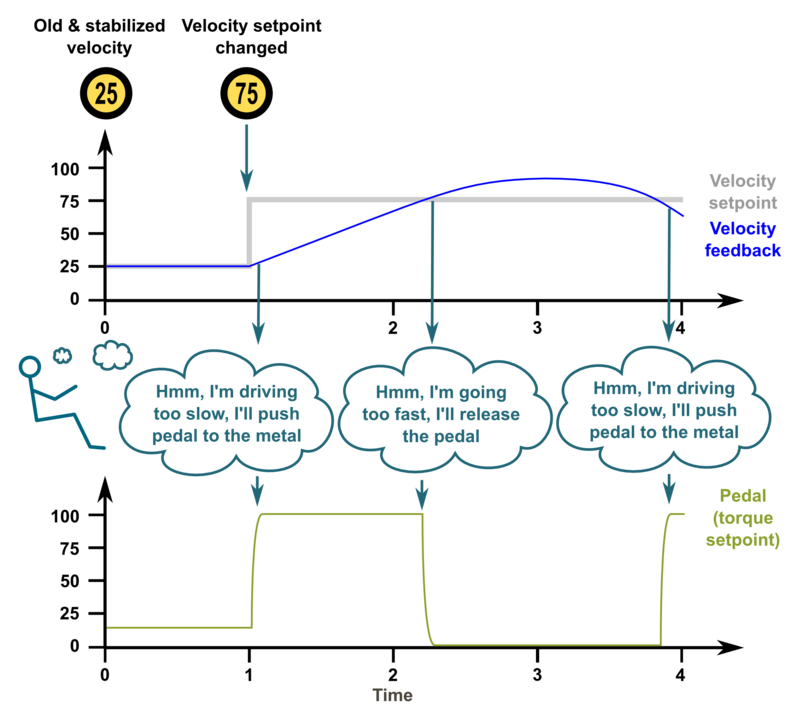
| + | ===Too high gains - oscillation & instability=== | ||
[[File:Carexample unstablepng.png|800px]] | [[File:Carexample unstablepng.png|800px]] | ||
| − | ===Optimum | + | |
| + | If the gains are set too high, the system becomes [[overshooting]], oscillating and less stable. Here the comparable PI gains could be P=200 I=100 | ||
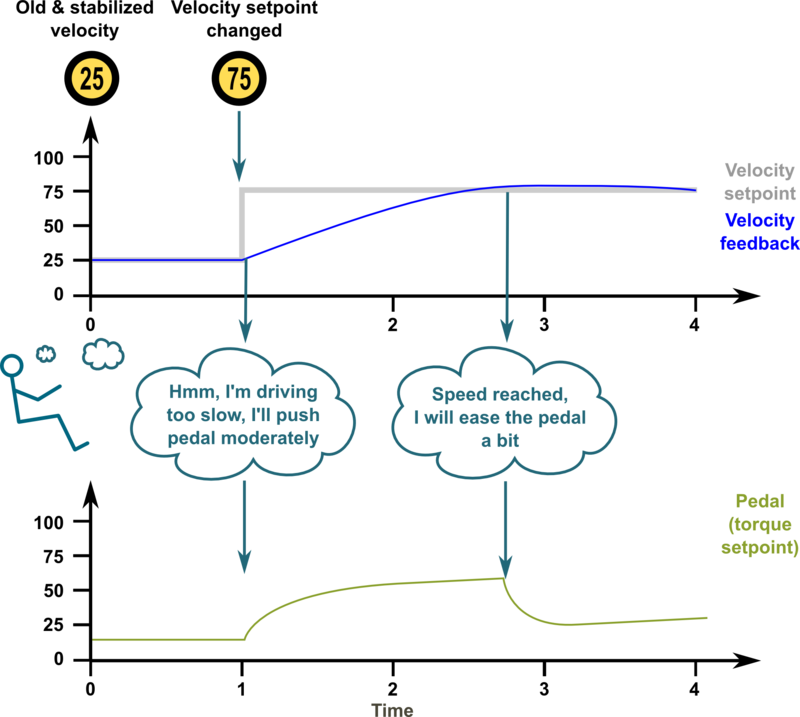
| + | ===Optimum gains - only little overshoot=== | ||
[[File:Carexample stable.png|800px]] | [[File:Carexample stable.png|800px]] | ||
| − | ===Optimum | + | |
| + | When the gains are tuned correctly, the response shows rapid response with low overshoot and no ringing or oscillations. The comparable gains here P=50 I=25. | ||
| + | ===Optimum gains with realistic setpoint - optimum response=== | ||
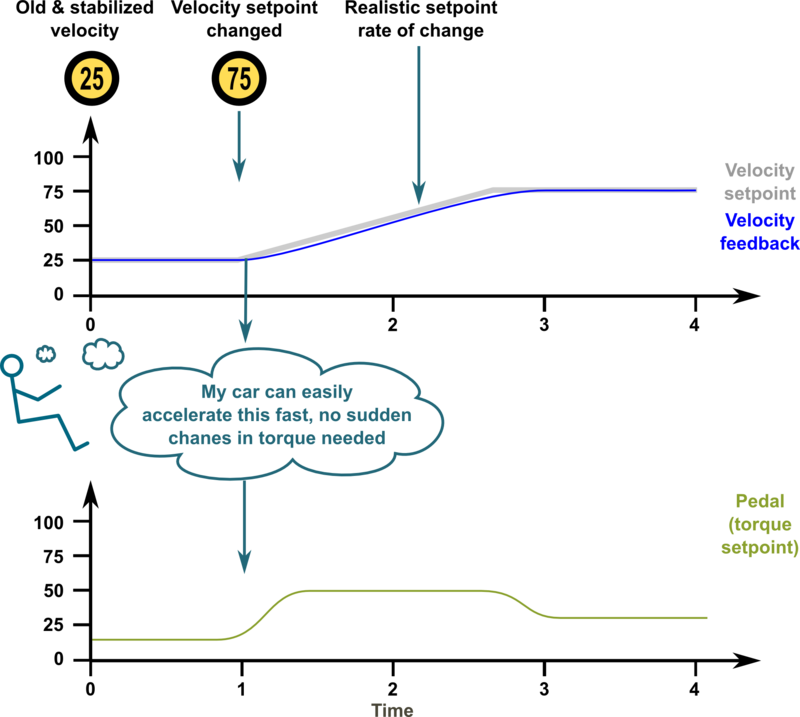
[[File:Carexample response accellimit.png|800px]] | [[File:Carexample response accellimit.png|800px]] | ||
| + | |||
| + | The response can be improved further by introducing a limit to the slew rate of setpoint signal. The controller behaves optimally when the system is able to follow the setpoint continuously with little tracking error. In this case the gains could be same as before, P=50 I=25. | ||
| + | |||
| + | ==Real servo motor controller== | ||
| + | See the principles of real world servo motor drive from article [[Signal path of motor drive]]. | ||
| + | {{next|[[Tuning torque controller]]}} | ||
| + | |||
| + | [[Category:Tuning_guide]] | ||
Latest revision as of 09:51, 29 June 2015
Driving a servo motor is much like driving a car. Driving a car has many similarities including the key concepts of torque, velocity and position control. Most of this happens in the driver's head the same way than a servo drive does with a motor.
For those who are already familiar with the basics, see the principles of real world servo motor drive from article Signal path of motor drive.
Contents
Driving (a.k.a servoing) a car[edit | edit source]
Driving a car to a destination is much like driving a servo motor to it's destination position. The analogies in between are:
| Car | Servo axis |
|---|---|
| Pedal (motor gasoline feed) | Torque setpoint (motor current feed) |
| Speed limit | Velocity setpoint |
| Target location | Position setpoint |
| Speed meter | Velocity feedback |
| Trip meter | Position feedback |
| Car driver | Servo drive |
The ultimate goal of driver is to get to the target. To achieve this, he follows the road (trajectory) at certain velocity and decelerates once target is being reached. Without knowing, the driver acts as servo controller where he:
- Controls car's velocity based on the speed meter value and speed limit
- Controls car's position based on trip meter's reading or by observing location trough the windshield
- All actions the driver makes, is based on comparing the setpoints and the actual state
Servo controller basics[edit | edit source]
Controller gains and a PI controller[edit | edit source]
Controller gain means sensitivity to change output due to tracking error (the difference between setpoint and feedback).
The simplest form of feedback based controller is a proportional gain controller (P controller) where output follows the formula output = Pgain*(setpoint-feedback). The problem of proportional gain controller is that it may never reach the setpoint because output starts approaching zero when the following error is reaching zero.
Because of this, it's better to add in integrating component to the controller (forming PI controller). Integrator accumulates the tracking error to a integrator variable. Integrator variable is like a bucket of water, when you add water, the water level rises and when you take out water, the level lowers. In controller the equation becomes: output = Pgain*(setpoint-feedback) + Igain*IntegralOf(setpoint-feedback).
The characteristics of feedback gain variables:
- P-gain - reacts instantly to the tracking error but can't eliminate tracking error completely
- I-gain - reacts slowly over time, adjusts output until tracking error is zero
When driving a car, human brain closely resembles the operation of a PI controller. For in-depth info about PI controllers and its variants, see the Wikipedia article PID controller.
Tuning the gains[edit | edit source]
Controller tuning means finding of the optimum gain values for the given system.
The proper gain values always depend on many aspects, especially the target system dynamic properties (such as motor properties, axis transmission ratios, inertias and masses). Change of properties introduces the requirement of tuning the gain values as gain values that work fine in one system may not behave satisfactory on a different system.
In servo drive case, this means that each motor type and mechanical axis need to be tuned separately. However, if axis and motors are identical, then the same gains should work equally.
Gain tuning (car) example[edit | edit source]
The following series of images illustrate an imaginary car driving scenario where the driver acts as velocity controller of the car. The magnitude of PI gain values equal the driver's aggressivity of controlling the pedal to reach the desired speed.
Low gains - sluggish response[edit | edit source]
If the gains are set too low, the system response tends to be sluggish and sometimes leave a static tracking error (not reaching setpoint in any time). In this imaginary case we could think PI gains to be P=20 I=10.
Too high gains - oscillation & instability[edit | edit source]
If the gains are set too high, the system becomes overshooting, oscillating and less stable. Here the comparable PI gains could be P=200 I=100
Optimum gains - only little overshoot[edit | edit source]
When the gains are tuned correctly, the response shows rapid response with low overshoot and no ringing or oscillations. The comparable gains here P=50 I=25.
Optimum gains with realistic setpoint - optimum response[edit | edit source]
The response can be improved further by introducing a limit to the slew rate of setpoint signal. The controller behaves optimally when the system is able to follow the setpoint continuously with little tracking error. In this case the gains could be same as before, P=50 I=25.
Real servo motor controller[edit | edit source]
See the principles of real world servo motor drive from article Signal path of motor drive.
| Read next |