Difference between revisions of "Servo tuning basics"
| [checked revision] | [checked revision] |
(→What is a feedback gain and PI controller) |
|||
| Line 11: | Line 11: | ||
Because of this, it's better to add in '''integrating''' component to the controller (forming PI controller). Integrator accumulates the tracking error to a integrator variable. Integrator variable is like a bucket of water, when you add water, the water level rises and when you take out water, the level lowers. In controller the equation becomes: ''output = Pgain*(setpoint-feedback) + Igain*IntegralOf(setpoint-feedback)''. | Because of this, it's better to add in '''integrating''' component to the controller (forming PI controller). Integrator accumulates the tracking error to a integrator variable. Integrator variable is like a bucket of water, when you add water, the water level rises and when you take out water, the level lowers. In controller the equation becomes: ''output = Pgain*(setpoint-feedback) + Igain*IntegralOf(setpoint-feedback)''. | ||
| − | The characteristics of gain variables: | + | The characteristics of feedback gain variables: |
*P-gain - reacts instantly to the tracking error but can't eliminate tracking error completely | *P-gain - reacts instantly to the tracking error but can't eliminate tracking error completely | ||
| − | *I-gain - reacts slowly over time | + | *I-gain - reacts slowly over time, adjusts output until tracking error is zero |
| − | When driving a car, human brain closely resembles the operation of PI controller. | + | When driving a car, human brain closely resembles the operation of a PI controller. |
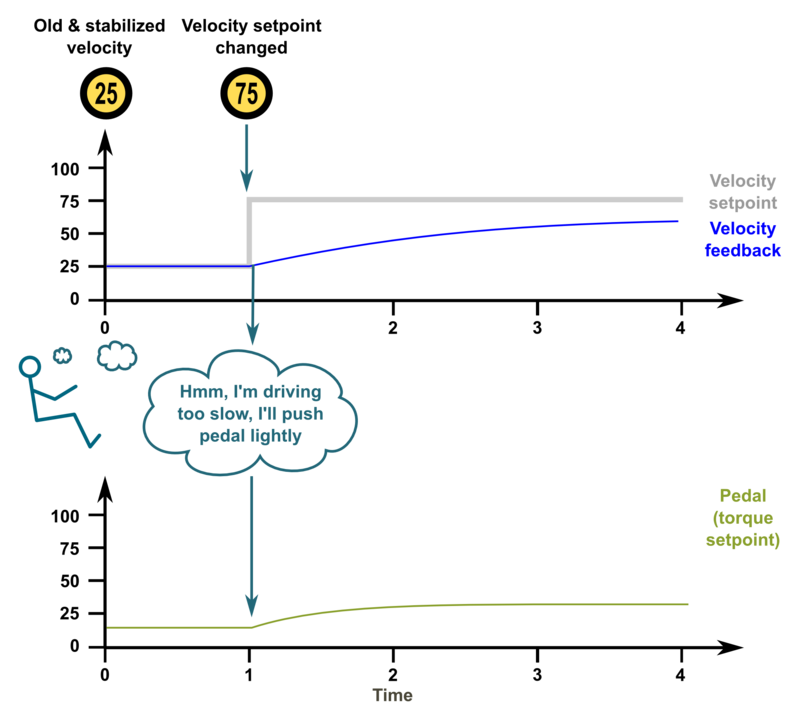
| − | ===Low feedback | + | ===Low feedback gains, sluggish response=== |
[[File:Carexample sluggish.png|800px]] | [[File:Carexample sluggish.png|800px]] | ||
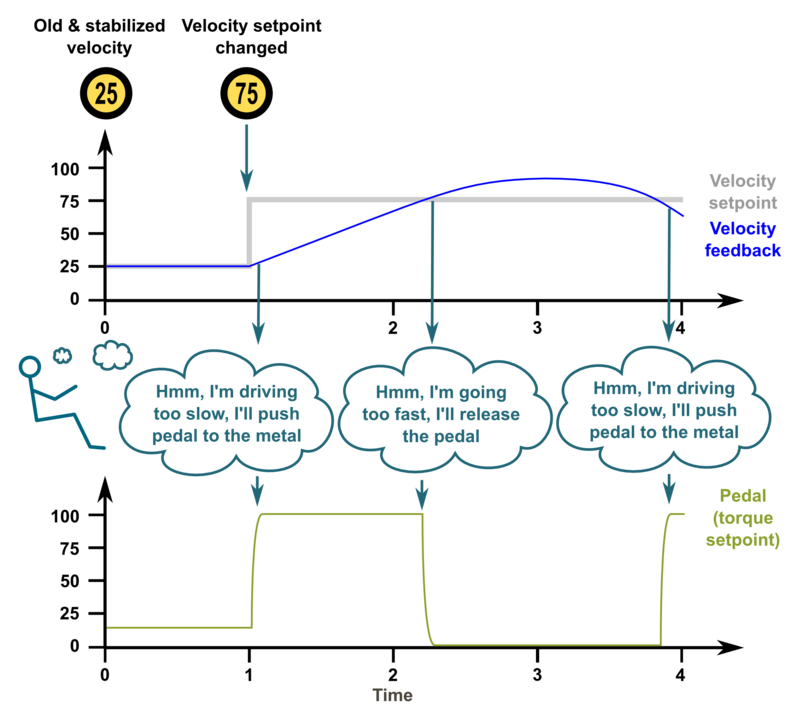
| − | ===Too high feedback | + | ===Too high feedback gains, oscillation & instability=== |
[[File:Carexample unstablepng.png|800px]] | [[File:Carexample unstablepng.png|800px]] | ||
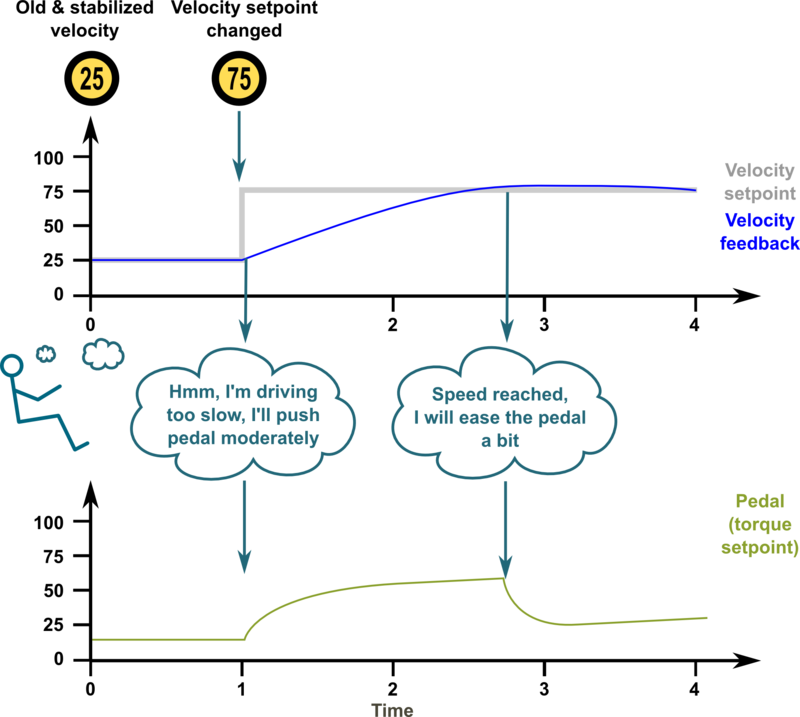
| − | ===Optimum feedback | + | ===Optimum feedback gains, only little overshoot=== |
[[File:Carexample stable.png|800px]] | [[File:Carexample stable.png|800px]] | ||
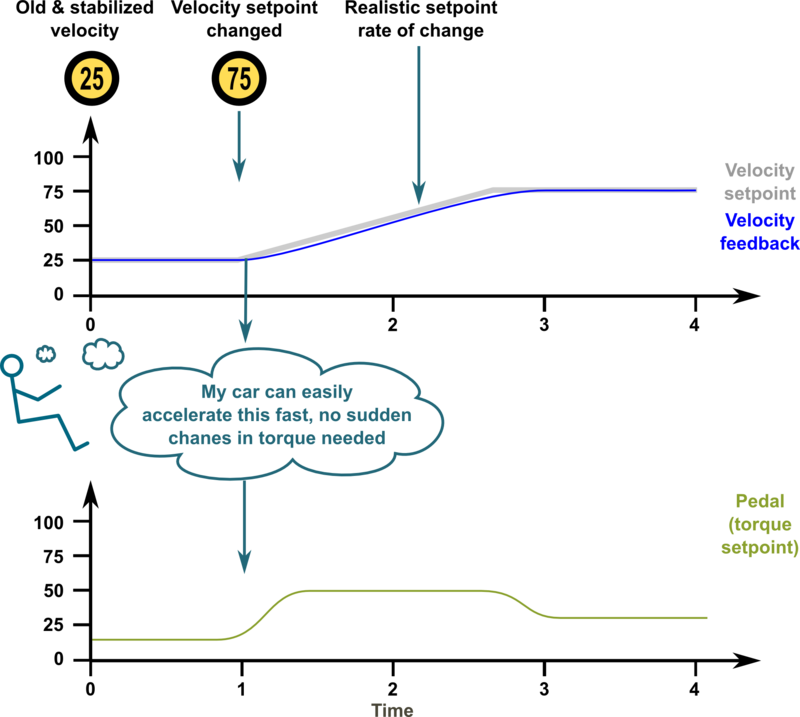
| − | ===Optimum | + | ===Optimum gains with realistic setpoint, optimum response=== |
[[File:Carexample response accellimit.png|800px]] | [[File:Carexample response accellimit.png|800px]] | ||
Revision as of 10:40, 12 August 2013
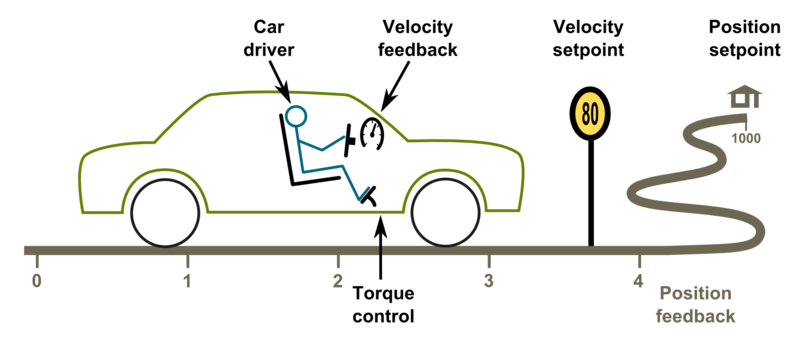
Driving a servo motor is much like driving a car. Driving a car has many similarities including the key concepts of torque, velocity and position control. Most of this happens in the driver's head the same way than a servo drive does with a motor.
Driving (a.k.a servoing) a car
Driver as a controller
What is a feedback gain and PI controller
Feedback gain means sensitivity to change output due to tracking error (the difference between setpoint and feedback).
The simplest form of feedback controller is a proportional gain controller (P controller) where output follows the formula output = Pgain*(setpoint-feedback). The problem of proportional gain controller is that it may never reach the setpoint because output starts approaching zero when the following error is reaching zero.
Because of this, it's better to add in integrating component to the controller (forming PI controller). Integrator accumulates the tracking error to a integrator variable. Integrator variable is like a bucket of water, when you add water, the water level rises and when you take out water, the level lowers. In controller the equation becomes: output = Pgain*(setpoint-feedback) + Igain*IntegralOf(setpoint-feedback).
The characteristics of feedback gain variables:
- P-gain - reacts instantly to the tracking error but can't eliminate tracking error completely
- I-gain - reacts slowly over time, adjusts output until tracking error is zero
When driving a car, human brain closely resembles the operation of a PI controller.
Low feedback gains, sluggish response
Too high feedback gains, oscillation & instability
Optimum feedback gains, only little overshoot
Optimum gains with realistic setpoint, optimum response
