Difference between revisions of "Servo tuning basics"
| [checked revision] | [checked revision] |
| Line 5: | Line 5: | ||
==Driver as a controller== | ==Driver as a controller== | ||
===What is a feedback gain=== | ===What is a feedback gain=== | ||
| − | Feedback gain means '''sensitivity to change output''' due to ''tracking error'' (the difference between setpoint and feedback) | + | Feedback gain means '''sensitivity to change output''' due to ''tracking error'' (the difference between setpoint and feedback). |
| − | Because of this, it's better to add in '''integrating | + | The simplest form of feedback controller is a '''proportional''' gain controller (P-gain) where output follows the formula ''output = Pgain*(setpoint-feedback)''. The problem of proportional gain controller is that it may never reach the setpoint because output starts approaching zero when the following error is reaching zero. |
| + | |||
| + | Because of this, it's better to add in '''integrating''' component to the controller. Integrator accumulates the tracking error to a integrator variable. Integrator variable is like a bucket of water, when you add water, the water level rises and when you take out water, the level lowers. In controller the equation becomes: ''output = Pgain*(setpoint-feedback) + Igain*IntegralOf(setpoint-feedback)''. | ||
The characteristics of gain variables: | The characteristics of gain variables: | ||
Revision as of 08:51, 12 August 2013
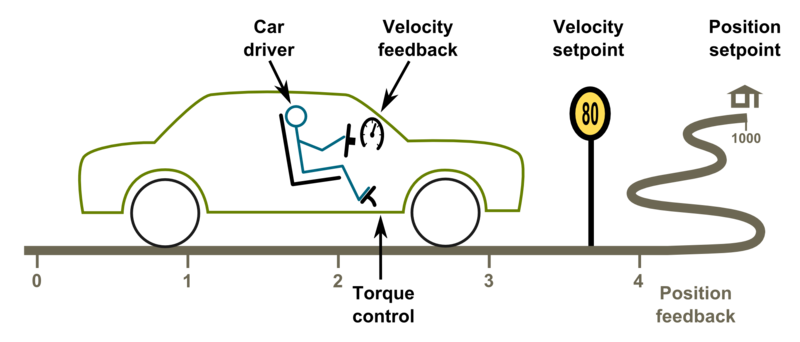
Driving a servo motor is much like driving a car. Driving a car has many similarities including the key concepts of torque, velocity and position control. Most of this happens in the driver's head the same way than a servo drive does with a motor.
Contents
Driving (a.k.a servoing) a car
Driver as a controller
What is a feedback gain
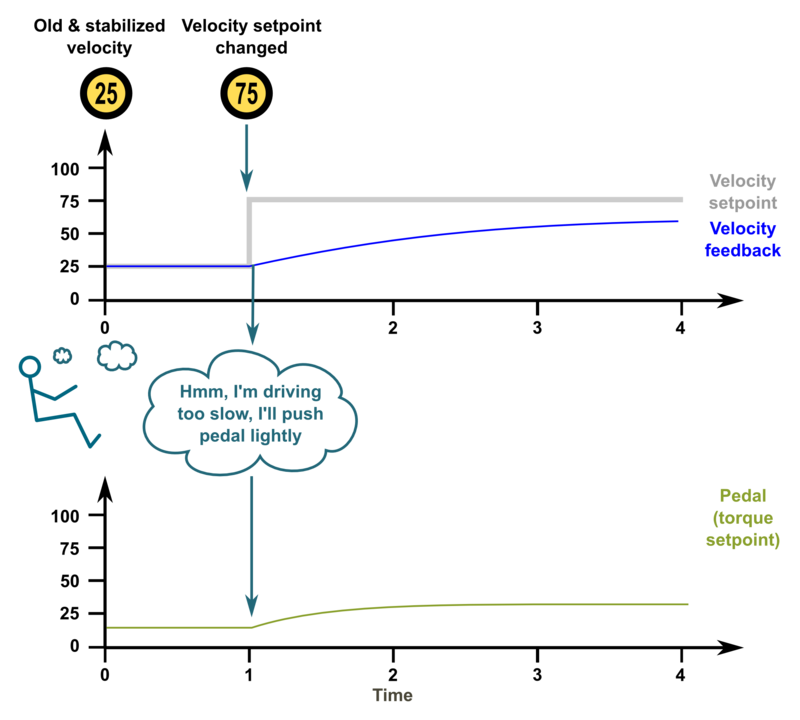
Feedback gain means sensitivity to change output due to tracking error (the difference between setpoint and feedback).
The simplest form of feedback controller is a proportional gain controller (P-gain) where output follows the formula output = Pgain*(setpoint-feedback). The problem of proportional gain controller is that it may never reach the setpoint because output starts approaching zero when the following error is reaching zero.
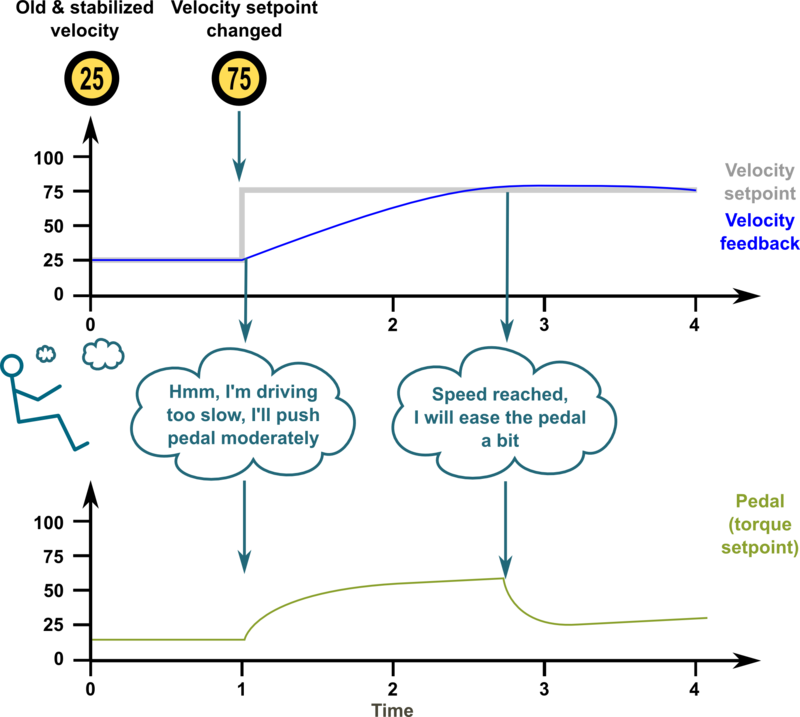
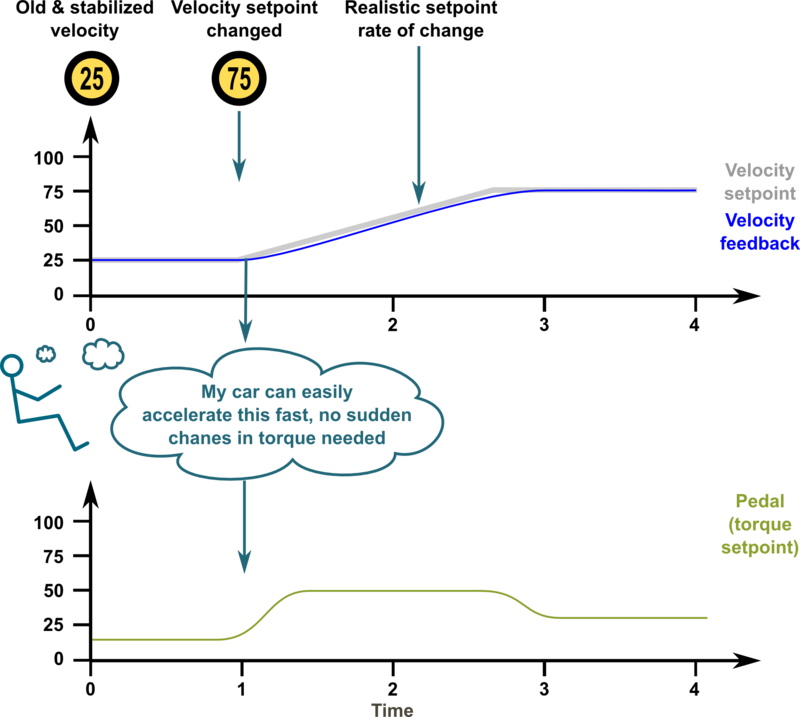
Because of this, it's better to add in integrating component to the controller. Integrator accumulates the tracking error to a integrator variable. Integrator variable is like a bucket of water, when you add water, the water level rises and when you take out water, the level lowers. In controller the equation becomes: output = Pgain*(setpoint-feedback) + Igain*IntegralOf(setpoint-feedback).
The characteristics of gain variables:
- P-gain - reacts instantly to the tracking error but can't eliminate tracking error completely
- I-gain - reacts slowly over time to the accumulated error, adjusts output until tracking error is dead zero
Low feedback gain, sluggish response
Too high feedback gain, oscillation & instability
Optimum feedback gain, only little overshoot
Optimum gain with realistic setpoint, optimum response
